6.4 Sets of intervals (interval_set)
interval_set I
1. Definition
An instance S of the parameterized data type is a
collection of items (is ). Every item in S contains a closed
interval of the real numbers as key and an information from data type I,
called the information type of S. The number of items in S is called
the size of S. An interval set of size zero is said to be empty. We use
< x, y, i > to denote the item with interval [x, y] and information i,
x (y) is called the left (right) boundary of the item. For each
interval
[x, y]⊂
). Every item in S contains a closed
interval of the real numbers as key and an information from data type I,
called the information type of S. The number of items in S is called
the size of S. An interval set of size zero is said to be empty. We use
< x, y, i > to denote the item with interval [x, y] and information i,
x (y) is called the left (right) boundary of the item. For each
interval
[x, y]⊂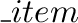 there is at most one item
< x, y, i > ∈S.
there is at most one item
< x, y, i > ∈S.
2. Creation
S
creates an instance of type and initializes to the
empty set.
3. Operations
& truecm & truecm &
double left is_item it
returns the left boundary of item it.
it is an item in .
double right is_item it
returns the right boundary of item it.
it is an item in .
I inf is_item it
returns the information of item it.
it is an item in .
is_item insert double x, double y, I i
associates the information i with interval
[x, y]. If there is an item < x, y, j > in
then j is replaced by i, else a new item
< x, y, i > is added to S. In both cases
the item is returned.
is_item lookup double x, double y
returns the item with interval [x, y]
(nil if no such item exists in ).
listis_item intersection double a, double b
returns all items
< x, y, i > ∈ S with
[x, y]∩[a, b]≠∅.
void del double x, double y
deletes the item with interval [x, y]
from .
void del_item is_item it
removes item it from .
it is an item in .
void change_inf is_item it, I i
makes i the information of item it.
it is an item in .
void clear
makes the empty interval_set.
bool empty
returns true iff is empty.
int size
returns the size of .
4. Implementation
Interval sets are implemented by two-dimensional range trees [Wi85, Lu78].
Operations insert, lookup, del_item and del take time
O(log2n),
intersection takes time
O(k + log2n), where k is the size
of the returned list. Operations left, right, inf, empty, and size
take time O(1), and clear
O(n log n). Here n is always the
current size of the interval set. The space requirement is
O(n log n).
 ). Every item in S contains a closed
interval of the real numbers as key and an information from data type I,
called the information type of S. The number of items in S is called
the size of S. An interval set of size zero is said to be empty. We use
< x, y, i > to denote the item with interval [x, y] and information i,
x (y) is called the left (right) boundary of the item. For each
interval
[x, y]⊂
). Every item in S contains a closed
interval of the real numbers as key and an information from data type I,
called the information type of S. The number of items in S is called
the size of S. An interval set of size zero is said to be empty. We use
< x, y, i > to denote the item with interval [x, y] and information i,
x (y) is called the left (right) boundary of the item. For each
interval
[x, y]⊂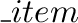 there is at most one item
< x, y, i > ∈S.
there is at most one item
< x, y, i > ∈S.